Adik-adik.. apa yang kalian bayangkan ketika mendengar kata matriks? Kalian keinget sama sebuah film berjudul "the matriks" ya? hehe... tapi hari ini, kita mau belajar matriks bukan yang di film itu. Yuk... dicek contoh soal di bawah ini:
1. Diketahui matriks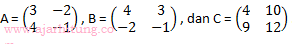 . Nilai determinan dari matriks (AB – C) adalah ...
. Nilai determinan dari matriks (AB – C) adalah ...
a. -7
b. -5
c. 2
d. 3
e. 12
Pembahasan:
Det (AB – C) = (12.1) – (9.1) = 12 – 9 = 3
Jawaban: D
2. Diketahui matriks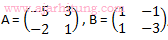 , invers matriks AB adalah ...
, invers matriks AB adalah ...
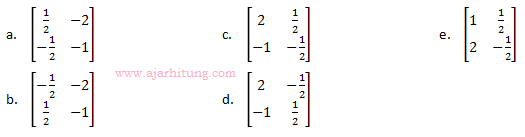
Pembahasan:
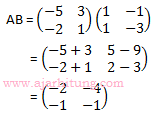
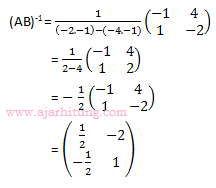
Jawaban: A
3. Matriks X yang memenuhi: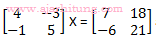 adalah ...
adalah ...
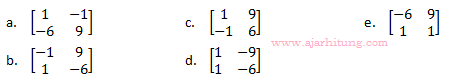
Pembahasan:
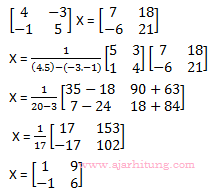
Jawaban: C
4. Jika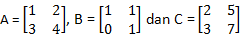 maka Det (AB + C) = ...
maka Det (AB + C) = ...
a. -8
b. -6
c. -2
d. 6
e. 8
Pembahasan:
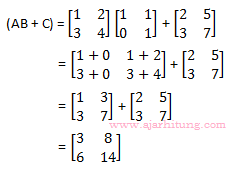
Det(AB + C) = (3.14) – (8.6) = 42 – 48 = -6
Jawaban: B
5. Diketahui matriks:
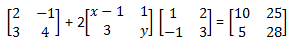
Nilai x + y adalah ...
a. 2
b. 6
c. 8
d. 10
e. 12
Pembahasan:
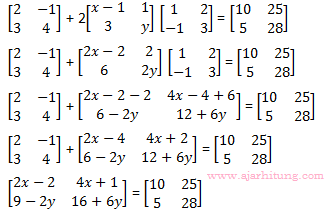
2x – 2 = 10
2x = 12
x = 6
9 – 2y = 5
-2y = -4
y = 2
Nilai x + y = 6 + 2 = 8
Jawaban: C
6. Matriks A =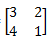 mempunyai hubungan dengan matriks B =
mempunyai hubungan dengan matriks B = 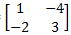 . Jika matriks C =
. Jika matriks C = 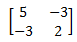 dan matriks D mempunyai hubungan yang serupa seperti A dengan B, maka matriks C + D adalah ...
dan matriks D mempunyai hubungan yang serupa seperti A dengan B, maka matriks C + D adalah ...
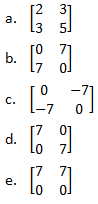
Pembahasan:
Hubungan matriks A dan B adalah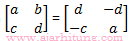
Sehingga jika C =
dan memiliki hubungan yang sama seperti A dan B dengan D, maka matriks D adalah: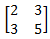
Jadi, nilai C + D = +
+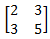 =
= 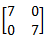
Jawaban: D
7. Jika matriks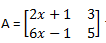 tidak mempunyai invers, maka nilai x adalah ...
tidak mempunyai invers, maka nilai x adalah ...
a. -2
b. -1
c. 0
d. 1
e. 2
Pembahasan:
Suatu matriks tidak memiliki invers jika determinan matriks tersebut adalah 0
Det (A) = 0
((2x + 1) 5) – ((6x – 1)3) = 0
10x + 5 – (18x – 3) = 0
10x + 5 – 18x + 3 = 0
-8x + 8 = 0
-8x = -8
x = 1
Jawaban: D
8. At adalah transpose dari A. Jika:
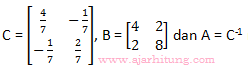 maka determinan dari matriks AtB adalah ...
maka determinan dari matriks AtB adalah ...
a. -196
b. -188
c. 188
d. 196
e. 21
Pembahasan:
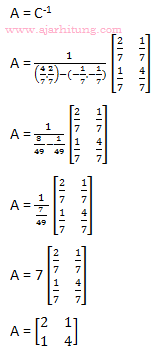

Det(AtB) = (10.34) – (12.12) = 340 – 144 = 196
Jawaban: D
9. Diketahui matriks-matriks :
 . Jika matriks C = A.B maka determinan matriks C adalah ...
. Jika matriks C = A.B maka determinan matriks C adalah ...
a. -66
b. -98
c. 80
d. 85
e. 98
Pembahasan:
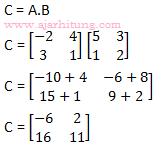
Det(C) = (-6.11) – (16.2) = -66 – 32 = -98
Jawaban: B
10. Jika M adalah matriks sehingga:
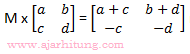 maka determinan matriks M adalah ...
maka determinan matriks M adalah ...
a. -2
b. -1
c. 0
d. 1
e. 2
Pembahasan:
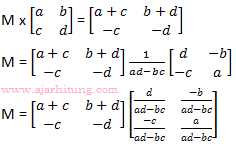
Det(M) = (1.-1) – (0.1) = -1 – 0 = -1
Jawaban: B
11. Jika
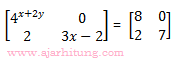 maka x + y adalah ...
maka x + y adalah ...
a. – 15/4
b. – 9/4
c. 9/4
d. 15/4
e. 5/4
Pembahasan:
3x – 2 = 7
3x = 9
x = 3
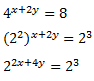
2x + 4y = 3
2 (3) + 4y = 3
6 + 4y = 3
4y = -3
y = - ¾
maka x + y = 3 – ¾ = 12/4 – ¾ = 9/4
Jawaban: C
12. Diketahui matriks
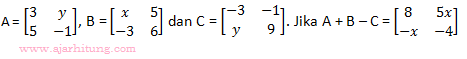 maka nilai x + 2xy + y adalah ...
maka nilai x + 2xy + y adalah ...
a. 8
b. 12
c. 18
d. 20
e. 22
Pembahasan: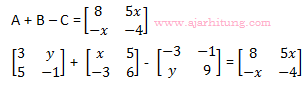
3 + x +3 = 8
6 + x = 8
x = 2
5 – 3 – y = -x
2 – y = -2
-y = -4
y = 4
maka nilai x + 2xy + y = 2 + 2.2.4 + 4 = 2 + 16 + 4 = 22
Jawaban: E
13. Jika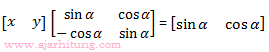 dan alpha suatu konstanta maka x + y = ...
dan alpha suatu konstanta maka x + y = ...
a. -2
b. -1
c. 0
d. 1
e. 2
Pembahasan:
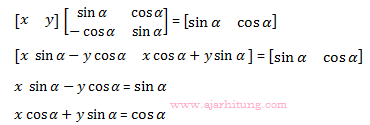
x = 1 dan y = 0
Nilai x + y = 1 + 0 = 1
Jawaban: D
14. Nilai p yang memenuhi persamaan matriks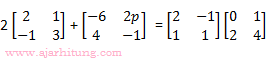 adalah ...
adalah ...
a. -2
b. -1
c. 0
d. 1
e. 2
Pembahasan:
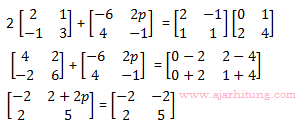
2 + 2p = -2
2p = -4
p = -2
Jawaban: A
15. Persamaan garis g dan garis h berturut-turut adalah Garis g dan garis h berpotongan di titik A, titik B (p, 1) terletak pada g, dan titik C (2, q) terletak pada garis h. Persamaan garis k yang melalui A dan sejajar BC adalah ...
Garis g dan garis h berpotongan di titik A, titik B (p, 1) terletak pada g, dan titik C (2, q) terletak pada garis h. Persamaan garis k yang melalui A dan sejajar BC adalah ...
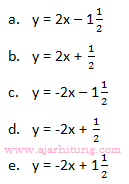
Pembahasan:
Garis g =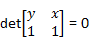
Garis g = y – x = 0 atau –x + y = 0
Garis h =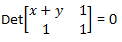
Garis h = x + y – 1 = 0 atau x + y = 1
Garis g dan h berpotongan di titik A, maka koordinat titik A adalah:
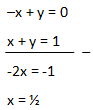
subtitusikan x = ½ dalam persamaan x + y = 1
x + y = 1
½ + y = 1
y = ½
titik A ( ½ , ½ )
titik B (p, 1) terletak pada g, maka:
–p + 1 = 0
p = 1
titik B (1, 1)
titik C (2, q) terletak pada garis h, maka:
2 + q = 1
q = -1
Titik C (2, -1)
Persamaan garis BC yang melalui titik B (1, 1) dan C (2, -1) adalah:

y – 1 = -2x + 2
2x + y = 3 atau y = – 2x + 3, maka gradien garis BC = -2
Maka, persamaan garis k adalah (m = -2 (karena sejajar dengan BC, melalui titik A ( ½ , ½ ) :
y – y1 = m (x – x1)
y – ½ = -2 (x – ½ )
y = -2x + 1 + ½
y = -2x + 1 1/2
Jawaban: E
16. jika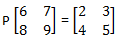 maka P = ...
maka P = ...
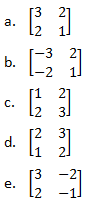
Pembahasan:
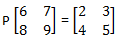
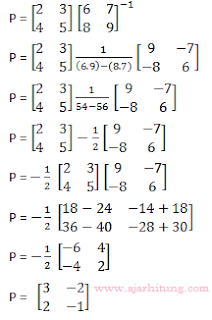
Jawaban: E
17. Jika P dan Q adalah matriks berordo 2 x 2 yang memenuhi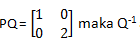 adalah...
adalah...

Pembahasan:
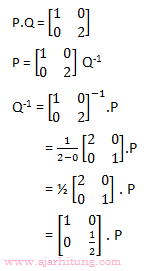
Jawaban: E
18. Jika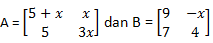 jika determinan A dan determinan B sama, maka harga x yang memenuhi adalah ...
jika determinan A dan determinan B sama, maka harga x yang memenuhi adalah ...
a. 3 atau 4
b. -3 atau -4
c. 3 atau -4
d. -4 atau -5
e. 3 atau -5
Pembahasan:
Det(A) = (5 + x) 3x – 5x =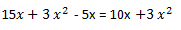
Det(B) = 9.4 – 7.(-x) = 36 + 7x
Det(A) = det(B)
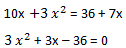
(3x – 9) (x + 4) = 0
x = 3 atau x = -4
Jawaban: C
19. Hasil kali semua nilai x sehingga matriks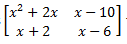 tidak mempunyai invers adalah ...
tidak mempunyai invers adalah ...
a. 20
b. -10
c. 10
d. -20
e. 9
Pembahasan:
Syarat suatu matriks tidak memiliki invers adalah jika determinan = 0, maka:
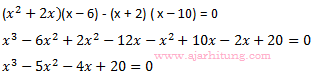
x1 . x2 . x3 = -d/a = -20/1 = -20
Jawaban: D
20. Dua garis dalam persamaan matriks: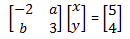 Saling tegak lurus jika a : b = ...
Saling tegak lurus jika a : b = ...
a. -6 : 1
b. -3 : 2
c. 1 : 1
d. 2 : 3
e. 1 : 2
Pembahasan:
Garis g = -2x + ay = 4
Garis h = bx + 3y = 12
mg = 2/a
mh = -b/3
karena g dan h saling tegak lurus, maka mg x mh = -1, maka:
2/a . –b/3 = -1
-2b/3a = -1
2b/3a = 1
3a = 2b
Sehingga a : b= 2 : 3
Jawaban: D
21. Matriks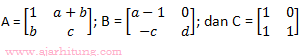 jika A + Bt = C dan Bt adalah transpose dari B, maka d = ...
jika A + Bt = C dan Bt adalah transpose dari B, maka d = ...
a. -1
b. -2
c. 0
d. 1
e. 2
Pembahasan:
A + Bt = C

a = 1
b =1
a+b-c =0
1 + 1 – c = 0
2 – c = 0
c = 2
c + d = 1
2 + d = 1
d = -1
Jawaban: A
22. Jika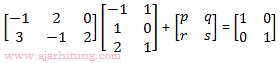 maka p + q + r + s = ...
maka p + q + r + s = ...
a. -5
b. -4
c. 3
d. 4
e. 5
Pembahasan:
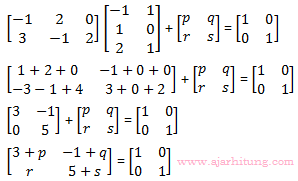
3 + p = 1
p = -2
-1 + q = 0
q = 1
r = 0
5 + s = 1
s = -4
p + q + r + s = -2 + 1 + 0 – 4 = -5
Jawaban: A
23. Diketahui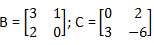 dan determinan dari B.C adalah K. Jika garis 2x – y = 5 dan x + y = 1 berpotongan di A, maka persamaan garis yang melalui A dan bergradien K adalah ...
dan determinan dari B.C adalah K. Jika garis 2x – y = 5 dan x + y = 1 berpotongan di A, maka persamaan garis yang melalui A dan bergradien K adalah ...
a. x – 12y + 25= 0
b. y – 12x + 25= 0
c. x + 12y + 11= 0
d. y – 12x - 11= 0
e. y – 12x + 11= 0
Pembahasan:
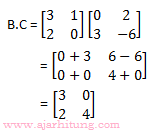
K = det(BC) = (3.4) – (2.0) = 12 – 0 = 12
Kita cari titik A:
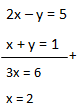
subtitusikan x = 2 dalam persamaan x + y = 1
x + y = 1
2 + y = 1
y = -1
Titik A (2, -1)
Persamaan garis bergradien k dan melalui titik A adalah:
y – y1 = m (x – x1)
y + 1 = 12 (x – 2)
y + 1 = 12x – 24
y – 12x = -25 atau y – 12x + 25 = 0
Jawaban: B
24. Jika M matriks berordo 2 x 2 dan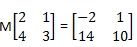 maka matriks M2 adalah ...
maka matriks M2 adalah ...
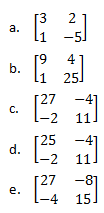
Pembahasan:
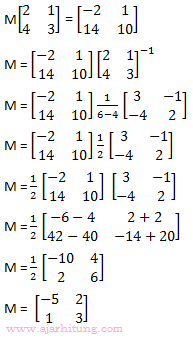
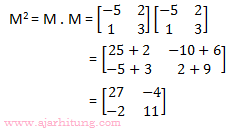
Jawaban: C
25. Jika matriks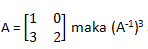 adalah matriks ...
adalah matriks ...
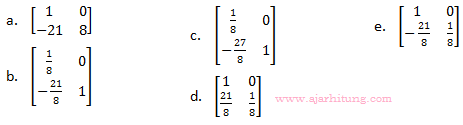
Pembahasan:
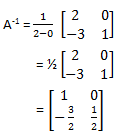

Jawaban: E
1. Diketahui matriks
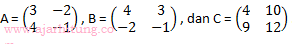 . Nilai determinan dari matriks (AB – C) adalah ...
. Nilai determinan dari matriks (AB – C) adalah ...a. -7
b. -5
c. 2
d. 3
e. 12
Pembahasan:
Det (AB – C) = (12.1) – (9.1) = 12 – 9 = 3
Jawaban: D
2. Diketahui matriks
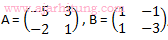 , invers matriks AB adalah ...
, invers matriks AB adalah ...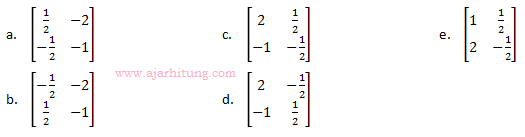
Pembahasan:
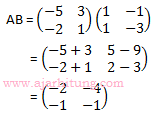
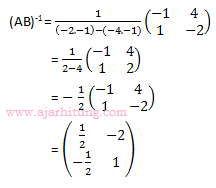
Jawaban: A
3. Matriks X yang memenuhi:
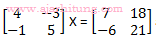 adalah ...
adalah ...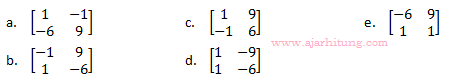
Pembahasan:
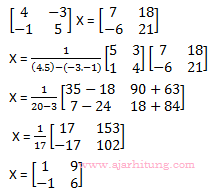
Jawaban: C
4. Jika
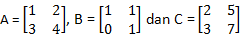 maka Det (AB + C) = ...
maka Det (AB + C) = ...a. -8
b. -6
c. -2
d. 6
e. 8
Pembahasan:
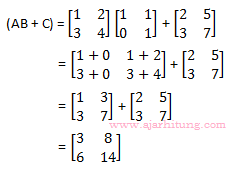
Det(AB + C) = (3.14) – (8.6) = 42 – 48 = -6
Jawaban: B
5. Diketahui matriks:
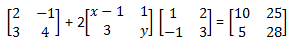
Nilai x + y adalah ...
a. 2
b. 6
c. 8
d. 10
e. 12
Pembahasan:
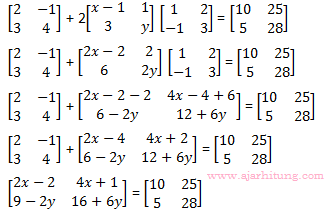
2x – 2 = 10
2x = 12
x = 6
9 – 2y = 5
-2y = -4
y = 2
Nilai x + y = 6 + 2 = 8
Jawaban: C
6. Matriks A =
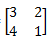 mempunyai hubungan dengan matriks B =
mempunyai hubungan dengan matriks B = 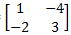 . Jika matriks C =
. Jika matriks C = 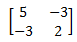 dan matriks D mempunyai hubungan yang serupa seperti A dengan B, maka matriks C + D adalah ...
dan matriks D mempunyai hubungan yang serupa seperti A dengan B, maka matriks C + D adalah ... 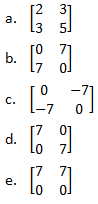
Pembahasan:
Hubungan matriks A dan B adalah
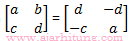
Sehingga jika C =

dan memiliki hubungan yang sama seperti A dan B dengan D, maka matriks D adalah:
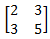
Jadi, nilai C + D =
 +
+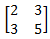 =
= 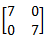
Jawaban: D
7. Jika matriks
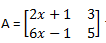 tidak mempunyai invers, maka nilai x adalah ...
tidak mempunyai invers, maka nilai x adalah ...a. -2
b. -1
c. 0
d. 1
e. 2
Pembahasan:
Suatu matriks tidak memiliki invers jika determinan matriks tersebut adalah 0
Det (A) = 0
((2x + 1) 5) – ((6x – 1)3) = 0
10x + 5 – (18x – 3) = 0
10x + 5 – 18x + 3 = 0
-8x + 8 = 0
-8x = -8
x = 1
Jawaban: D
8. At adalah transpose dari A. Jika:
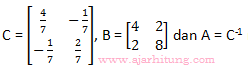 maka determinan dari matriks AtB adalah ...
maka determinan dari matriks AtB adalah ...a. -196
b. -188
c. 188
d. 196
e. 21
Pembahasan:
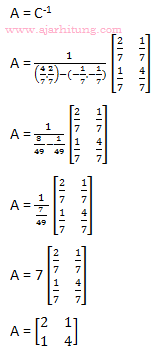

Det(AtB) = (10.34) – (12.12) = 340 – 144 = 196
Jawaban: D
9. Diketahui matriks-matriks :
 . Jika matriks C = A.B maka determinan matriks C adalah ...
. Jika matriks C = A.B maka determinan matriks C adalah ...a. -66
b. -98
c. 80
d. 85
e. 98
Pembahasan:
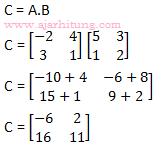
Det(C) = (-6.11) – (16.2) = -66 – 32 = -98
Jawaban: B
10. Jika M adalah matriks sehingga:
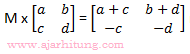 maka determinan matriks M adalah ...
maka determinan matriks M adalah ...a. -2
b. -1
c. 0
d. 1
e. 2
Pembahasan:
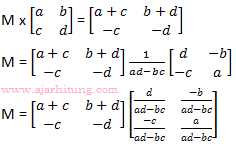
Det(M) = (1.-1) – (0.1) = -1 – 0 = -1
Jawaban: B
11. Jika
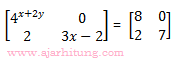 maka x + y adalah ...
maka x + y adalah ...a. – 15/4
b. – 9/4
c. 9/4
d. 15/4
e. 5/4
Pembahasan:
3x – 2 = 7
3x = 9
x = 3
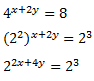
2x + 4y = 3
2 (3) + 4y = 3
6 + 4y = 3
4y = -3
y = - ¾
maka x + y = 3 – ¾ = 12/4 – ¾ = 9/4
Jawaban: C
12. Diketahui matriks
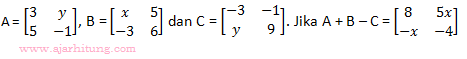 maka nilai x + 2xy + y adalah ...
maka nilai x + 2xy + y adalah ...a. 8
b. 12
c. 18
d. 20
e. 22
Pembahasan:
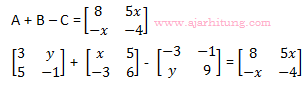
3 + x +3 = 8
6 + x = 8
x = 2
5 – 3 – y = -x
2 – y = -2
-y = -4
y = 4
maka nilai x + 2xy + y = 2 + 2.2.4 + 4 = 2 + 16 + 4 = 22
Jawaban: E
13. Jika
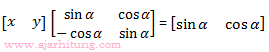 dan alpha suatu konstanta maka x + y = ...
dan alpha suatu konstanta maka x + y = ...a. -2
b. -1
c. 0
d. 1
e. 2
Pembahasan:
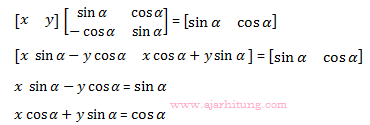
x = 1 dan y = 0
Nilai x + y = 1 + 0 = 1
Jawaban: D
14. Nilai p yang memenuhi persamaan matriks
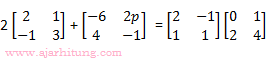 adalah ...
adalah ...a. -2
b. -1
c. 0
d. 1
e. 2
Pembahasan:
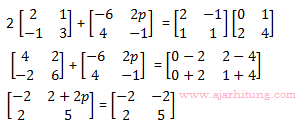
2 + 2p = -2
2p = -4
p = -2
Jawaban: A
15. Persamaan garis g dan garis h berturut-turut adalah
 Garis g dan garis h berpotongan di titik A, titik B (p, 1) terletak pada g, dan titik C (2, q) terletak pada garis h. Persamaan garis k yang melalui A dan sejajar BC adalah ...
Garis g dan garis h berpotongan di titik A, titik B (p, 1) terletak pada g, dan titik C (2, q) terletak pada garis h. Persamaan garis k yang melalui A dan sejajar BC adalah ...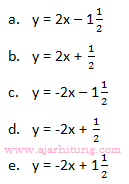
Pembahasan:
Garis g =
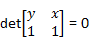
Garis g = y – x = 0 atau –x + y = 0
Garis h =
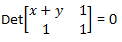
Garis h = x + y – 1 = 0 atau x + y = 1
Garis g dan h berpotongan di titik A, maka koordinat titik A adalah:
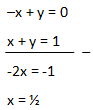
subtitusikan x = ½ dalam persamaan x + y = 1
x + y = 1
½ + y = 1
y = ½
titik A ( ½ , ½ )
titik B (p, 1) terletak pada g, maka:
–p + 1 = 0
p = 1
titik B (1, 1)
titik C (2, q) terletak pada garis h, maka:
2 + q = 1
q = -1
Titik C (2, -1)
Persamaan garis BC yang melalui titik B (1, 1) dan C (2, -1) adalah:

y – 1 = -2x + 2
2x + y = 3 atau y = – 2x + 3, maka gradien garis BC = -2
Maka, persamaan garis k adalah (m = -2 (karena sejajar dengan BC, melalui titik A ( ½ , ½ ) :
y – y1 = m (x – x1)
y – ½ = -2 (x – ½ )
y = -2x + 1 + ½
y = -2x + 1 1/2
Jawaban: E
16. jika
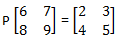 maka P = ...
maka P = ...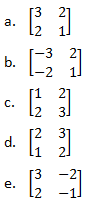
Pembahasan:
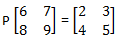
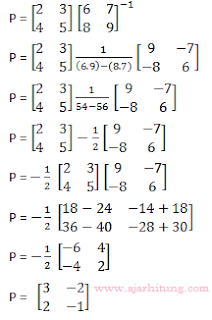
Jawaban: E
17. Jika P dan Q adalah matriks berordo 2 x 2 yang memenuhi
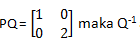 adalah...
adalah...
Pembahasan:
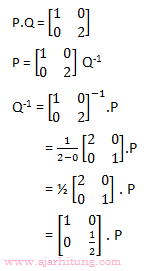
Jawaban: E
18. Jika
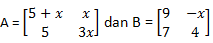 jika determinan A dan determinan B sama, maka harga x yang memenuhi adalah ...
jika determinan A dan determinan B sama, maka harga x yang memenuhi adalah ...a. 3 atau 4
b. -3 atau -4
c. 3 atau -4
d. -4 atau -5
e. 3 atau -5
Pembahasan:
Det(A) = (5 + x) 3x – 5x =
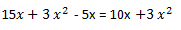
Det(B) = 9.4 – 7.(-x) = 36 + 7x
Det(A) = det(B)
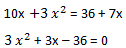
(3x – 9) (x + 4) = 0
x = 3 atau x = -4
Jawaban: C
19. Hasil kali semua nilai x sehingga matriks
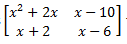 tidak mempunyai invers adalah ...
tidak mempunyai invers adalah ...a. 20
b. -10
c. 10
d. -20
e. 9
Pembahasan:
Syarat suatu matriks tidak memiliki invers adalah jika determinan = 0, maka:
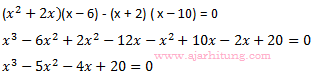
x1 . x2 . x3 = -d/a = -20/1 = -20
Jawaban: D
20. Dua garis dalam persamaan matriks:
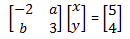 Saling tegak lurus jika a : b = ...
Saling tegak lurus jika a : b = ...a. -6 : 1
b. -3 : 2
c. 1 : 1
d. 2 : 3
e. 1 : 2
Pembahasan:
Garis g = -2x + ay = 4
Garis h = bx + 3y = 12
mg = 2/a
mh = -b/3
karena g dan h saling tegak lurus, maka mg x mh = -1, maka:
2/a . –b/3 = -1
-2b/3a = -1
2b/3a = 1
3a = 2b
Sehingga a : b= 2 : 3
Jawaban: D
21. Matriks
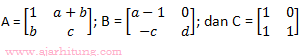 jika A + Bt = C dan Bt adalah transpose dari B, maka d = ...
jika A + Bt = C dan Bt adalah transpose dari B, maka d = ...a. -1
b. -2
c. 0
d. 1
e. 2
Pembahasan:
A + Bt = C

a = 1
b =1
a+b-c =0
1 + 1 – c = 0
2 – c = 0
c = 2
c + d = 1
2 + d = 1
d = -1
Jawaban: A
22. Jika
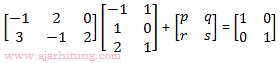 maka p + q + r + s = ...
maka p + q + r + s = ...a. -5
b. -4
c. 3
d. 4
e. 5
Pembahasan:
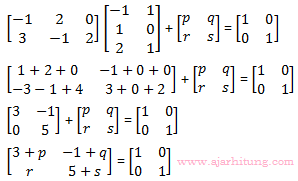
3 + p = 1
p = -2
-1 + q = 0
q = 1
r = 0
5 + s = 1
s = -4
p + q + r + s = -2 + 1 + 0 – 4 = -5
Jawaban: A
23. Diketahui
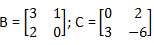 dan determinan dari B.C adalah K. Jika garis 2x – y = 5 dan x + y = 1 berpotongan di A, maka persamaan garis yang melalui A dan bergradien K adalah ...
dan determinan dari B.C adalah K. Jika garis 2x – y = 5 dan x + y = 1 berpotongan di A, maka persamaan garis yang melalui A dan bergradien K adalah ...a. x – 12y + 25= 0
b. y – 12x + 25= 0
c. x + 12y + 11= 0
d. y – 12x - 11= 0
e. y – 12x + 11= 0
Pembahasan:
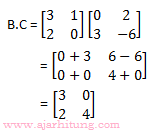
K = det(BC) = (3.4) – (2.0) = 12 – 0 = 12
Kita cari titik A:
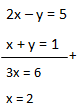
subtitusikan x = 2 dalam persamaan x + y = 1
x + y = 1
2 + y = 1
y = -1
Titik A (2, -1)
Persamaan garis bergradien k dan melalui titik A adalah:
y – y1 = m (x – x1)
y + 1 = 12 (x – 2)
y + 1 = 12x – 24
y – 12x = -25 atau y – 12x + 25 = 0
Jawaban: B
24. Jika M matriks berordo 2 x 2 dan
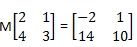 maka matriks M2 adalah ...
maka matriks M2 adalah ...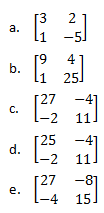
Pembahasan:
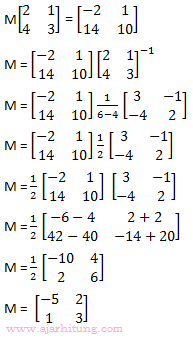
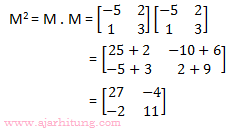
Jawaban: C
25. Jika matriks
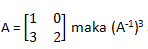 adalah matriks ...
adalah matriks ...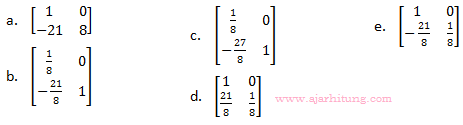
Pembahasan:
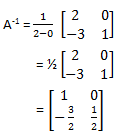

Jawaban: E


0 komentar:
Post a Comment