Pengertian Ekuivalen
Arti kata Ekuivalen dalam arti KBBI adalah mempunyai nilai (ukuran, arti, atau efek) yang sama. Tetapi jika arti dari Himpunan Ekuivalen adalah himpunan yang unsurnya tidak sama, tapi banyak anggotanya sama. Dan Himpunan Ekuivalen bisa berarti juga dua himpunan yang memiliki jumlah anggota sama.
Jadi, pada dasarnya Ekuivalen itu adalah mempunyai nilai yang sama walau ada beberapa nilai nilai didalamnya. Dan kami akan memberikan sedikit contoh soal dari Ekuivalen tersebut:
Contoh Soal Himpunan Ekuivalen
Dan, di Makalah Ekuivalen ini kita akan membahas 7 bagian bagian penting dari Ekuivalen tersebut. 7 Bagian itu adalah:
I. Rank suatu matriks
II. Transformasi elementer
III. Invers suatu matriks elementer
IV. Matriks-matriks yang ekwivalen
IV. Matriks-matriks yang ekwivalen
V. Bentuk kanonik suatu matriks
VI. Bnetuk Normal suatu matriks
VII. Matriks-matriks elementer
BAB 2
7 BAGIAN PEMBAHASAN EKUIVALEN
1. RANK SUATU MATRIKS
Definisi Matriks
Rank dari suatu matriks berukuran m×n adalah jumlah maksimum dari vektor baris atau kolom yang bebas linier atau independen linier. Rank dari suatu matriks merupakan dimensi dari vektor baris atau kolom non-zero pada matriks tersebut.
Pada matriks bujur sangkarA, jika vektor baris dan vektor kolom yang bebas linier mempunyai dimensi yang sama, maka dimensi matriks tersebut merupakan rank matriks.
Misalnya diketahui matriks berukuran m×n:
Rank dari matriks A dinyatakan oleh rank(A)atau r(A).
Notasi rank suatu matriks:
(rank(A)⟺r(A) )
Rank matriks dapat digunakan untuk mengetahui apakah suatu matriks itu singular atau nonsingular. Jika A matriks bujur sangkar dengan dimensi nxn, maka:
- Matriks A adalah nonsingular apabila rank(A)=n
- Matriks A adalah singular apabila rank(A)<n
Ada beberapa metode untuk menentukan rank dari suatu matriks yaitu minor matriks dan eliminasi Gauss (operasi baris elementer).
Sifat Rank Matriks
Ada beberapa sifat rank matriks yaitu:
- Jika matriks A berukuran mxn, maka:rank(A)=rank (A^T )
- Jika A matriks ukuran m×n, maka vektor baris matriks A adalah bebas linier jika dan hanya jikarank(A)=n
- Jika A matriks ukuranm×n,maka vektor kolom matriks A adalah bebas linier jika dan hanya jikarank(A)=m
2.TRANSFORMASI ELEMENTER
Yang dimaksud dengan transformai pada baris atau kolom suatu matriks A adalah sebagai berikut.
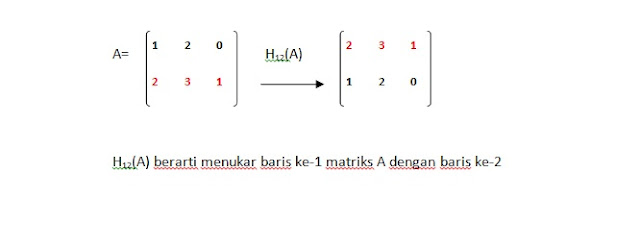
1. Penukaran tempat baris ke-i dan baris ke-j atau penukaran kolom ke-i dan kolom ke-j dan ditulis Hij(A) untuk transformasi baris dan Kij(A) untuk transformasi kolom.
Contoh :
a. Penukaran baris
b. Penukaran kolom
2. Memperkalikan baris ke-i dengan suatu bilangan skalar h0, ditulis Hi(h)(A) dan memperkalikan kolom ke-i dengan skalar k0, ditulis Ki(k)(A).
Contoh :
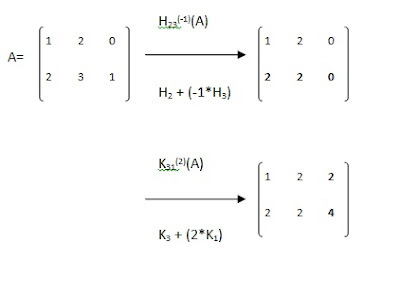
3. Menambah kolom ke-i dengan k kali koom ke-j, ditulis Kij(k)(A) dan menambah baris ke-i dengan h kali baris ke-j, ditulis Hij(h)(A).
Contoh :
3. INVERS SUATU MATRIKS ELEMENTER
Dua buah matriks A dan B disebut ekuivalen (A~B) apabila salah satunya dapat diperoleh dari yang lain dengan transformasi-transformasi elementer terhadap baris dan kolom. Kalau transformasi elementer hanya terjadi pada baris saja disebut ELEMENTER BARIS, sedangkan jika transformasi terjadi pada kolom saja disebut ELEMENTER KOLOM
4. MATRIKS MATRIKS YANG DI EKWIVALEN
Jika mengerjakan satu kali (single) tramsformasi elementer terhadap suatu matriks identitas maka hasil tranformasi elementer ini disebut matriks elementer
5. BENTUK KANONIK SUATU MATRIKS
Bentuk Kanonik suatu Matriks adalah matriks dgn sifat :
- Elemen pada setiap r baris pertama tidak semuanya nol, sedangkan elemen pada baris yang lain, jika ada semuanya nol.
- Dalam bariske - i (i=1,2,3,…r), elemen tak nol yang pertama adalah 1. (sebut kolom yang memuatnya dengan kolomke-ji)
- Satu-satu nya elemen tak nol pada kolom ke - ji adalah 1.
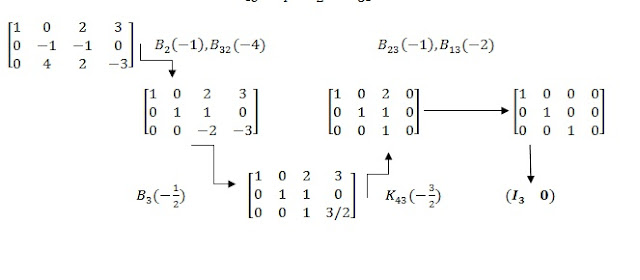
Dalam mengubah suatu matriks A ke matriks Kanonik dapat digunakan :
6. BENTUK NORMAL SUATU MATRIKS
Dengan menggunakan Transformasi elementer, setiap matriks nol A [r(A)=r] bias dibawa kebentuk normal N. [Transformasi elementer baris dan kolom dapat digunakan secara bersamaan.
7. MATRIKS ELEMENTER
Sebuah Matriks nxn dinamakan Matriks Elementer jika matriks tersebut dapat diperoleh dari matriks identitas (satuan) [I_n] dengan melakukan sebuah transformasi elementer tunggal.
Jenis-jenis Matriks Elementer
→ I_ij Matriks yang diperoleh dari matriks Identitas I, dengan menukarkan baris/kolom ke i dengan baris/kolom ke j.
→ I_i (k) Matriks yang diperoleh dari Matriks Identitas I, dengan menggandakan baris/kolom ke i dengan skalar K≠0.
→ I_ij (K) Matriks yang diperoleh dari Matriks Identitas I dengan (Baris ke i) + k (Baris ke j) atau (kolom ke j) + j (kolom ke i)
Contoh :
Sekian Dulu Semoga Bermanfaat :) :) :)


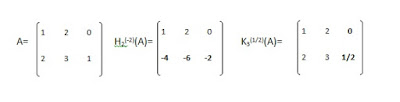





0 komentar:
Post a Comment